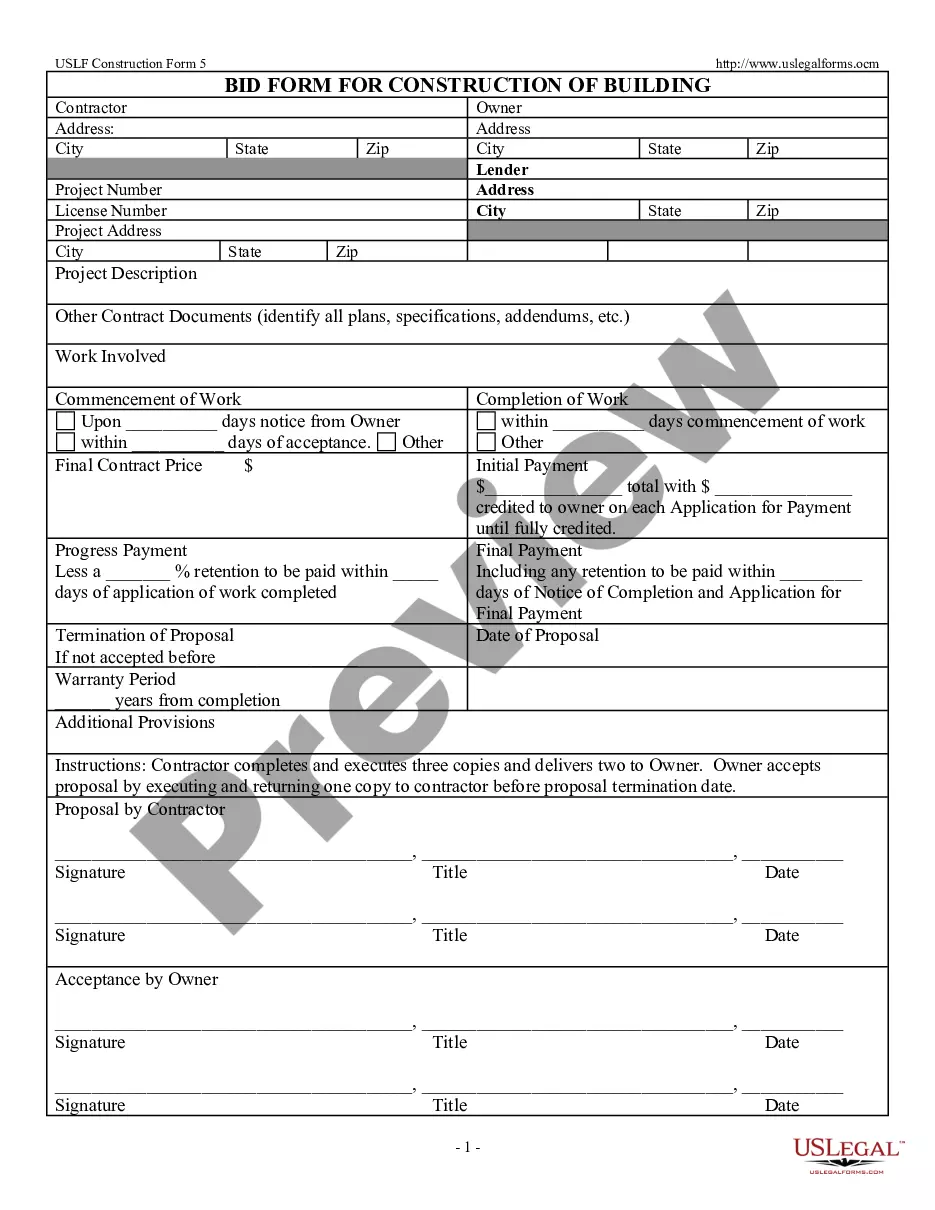
Closure Any Property For Regular Language In Montgomery
Description
Get your form ready online
Our built-in tools help you complete, sign, share, and store your documents in one place.
Make edits, fill in missing information, and update formatting in US Legal Forms—just like you would in MS Word.
Download a copy, print it, send it by email, or mail it via USPS—whatever works best for your next step.
Sign and collect signatures with our SignNow integration. Send to multiple recipients, set reminders, and more. Go Premium to unlock E-Sign.
If this form requires notarization, complete it online through a secure video call—no need to meet a notary in person or wait for an appointment.
We protect your documents and personal data by following strict security and privacy standards.
Make edits, fill in missing information, and update formatting in US Legal Forms—just like you would in MS Word.
Download a copy, print it, send it by email, or mail it via USPS—whatever works best for your next step.
Sign and collect signatures with our SignNow integration. Send to multiple recipients, set reminders, and more. Go Premium to unlock E-Sign.
If this form requires notarization, complete it online through a secure video call—no need to meet a notary in person or wait for an appointment.
We protect your documents and personal data by following strict security and privacy standards.
Looking for another form?
Form popularity
FAQ
The set of regular languages is closed under complementation. The complement of language L, written L, is all strings not in L but with the same alphabet. The statement says that if L is a regular lan- guage, then so is L. To see this fact, take deterministic FA for L and interchange the accept and reject states.
Regular languages are closed under concatenation - this is demonstrable by having the accepting state(s) of one language with an epsilon transition to the start state of the next language. If we consider the language L = {a^n | n >=0}, this language is regular (it is simply a).
Regular Languages are closed under intersection, i.e., if L1 and L2 are regular then L1 ∩ L2 is also regular. L1 and L2 are regular • L1 ∪ L2 is regular • Hence, L1 ∩ L2 = L1 ∪ L2 is regular.
The closure property states that if L1 and L2 are regular languages, then their union L1 ∪ L2 is also a regular language. This means that any string belonging to either L1 or L2, or both, can be recognized by a finite automaton or expressed using a regular expression.
Closure under intersection If L and M are regular languages, then so is L ∩ M. We assume that the alphabets of both automata are the same ; that is Σ is the union of the alphabets of L and M, if they are different.
Let L be a regular language, and M be an NFA that accepts it. Here, δR is δ with the direction of all the arcs reversed. Thus, it is proved that L is closed under reversal.
To prove if a language is a regular language, one can simply provide the finite state machine that generates it. If the finite state machine for a given language is not obvious (and this might certainly be the case if a language is, in fact, non-regular), the pumping lemma for regular languages is a useful tool.
Intersection. Theorem If L1 and L2 are regular languages, then the new language L = L1 ∩ L2 is regular. Proof By De Morgan's law, L = L1 ∩ L2 = L1 ∪ L2. By the previous two theorems this language is regular.
A regular language satisfies the following equivalent properties: it is the language of a regular expression (by the above definition) it is the language accepted by a nondeterministic finite automaton (NFA) it is the language accepted by a deterministic finite automaton (DFA)
Regular Languages are closed under intersection, i.e., if L1 and L2 are regular then L1 ∩ L2 is also regular. L1 and L2 are regular • L1 ∪ L2 is regular • Hence, L1 ∩ L2 = L1 ∪ L2 is regular.
