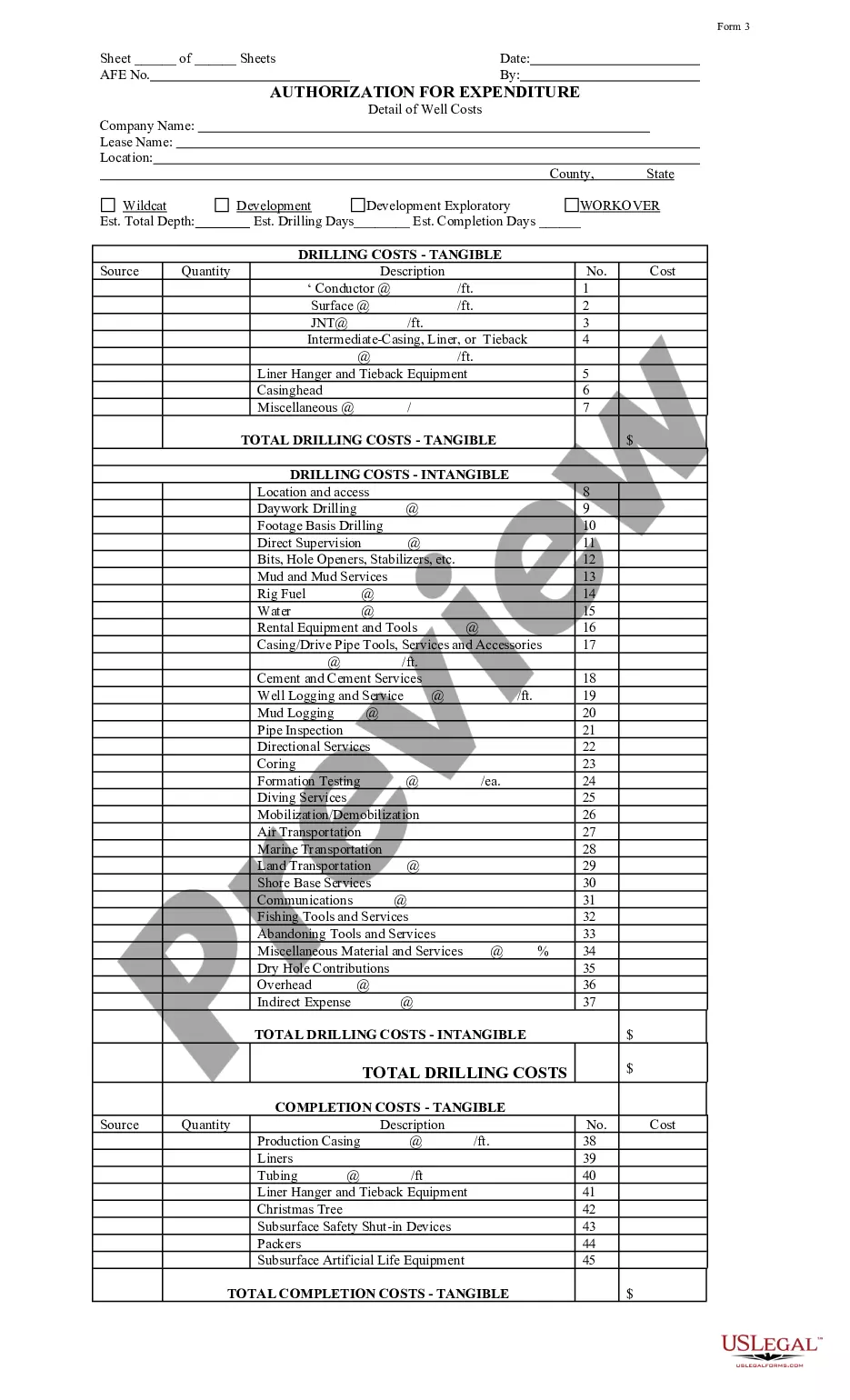
Agreement General Form For A Linear Equation In Florida
Description
Form popularity
FAQ
Standard Form of Linear Equation ax + b = 0, where, a ≠ 0 and x is the variable. ax + by + c = 0, where, a ≠ 0, b ≠ 0 , x and y are the variables. ax + by + cz + d = 0, where a ≠ 0, b ≠ 0, c ≠ 0, x, y, z are the variables.
Given a Linear equation, to put it into function form, just solve for y, that is, get everything on the right side of the equation except y. This is easily done. The result can be called y = mx + b, a.k.a. slope intercept form.
A linear function is of the form f(x) = mx + b where 'm' and 'b' are real numbers. Isn't it looking like the slope-intercept form of a line which is expressed as y = mx + b? Yes, this is because a linear function represents a line, i.e., its graph is a line.
For example, y = 3x - 2 represents a straight line on a coordinate plane and hence it represents a linear function. Since y can be replaced with f(x), this function can be written as f(x) = 3x - 2.
Writing Linear Equations as Functions Another way to write y = mx + b is f(x) = mx + b. It means that there is a function of x which is in the form f(x) = mx + b. f(x) is the same as the y-value at point x. We can call this function anything, it does not have to be f(x), it can be g(x), h(x), and so on.
Given a Linear equation, to put it into function form, just solve for y, that is, get everything on the right side of the equation except y. This is easily done. The result can be called y = mx + b, a.k.a. slope intercept form.
General form of a line The general form ax+by+c=0 is one of the many different forms you can write linear functions in. Other ones include the slope intercept form y=mx+b or slope-point form. We can convert the linear function among different forms.
How do you determine a linear function? A linear function is expressed by the equation y=mx+b, where y is the dependent variable, m is the slope, x is the independent variable, and b is the y-intercept.
The standard form for linear equations in two variables is Ax+By=C. For example, 2x+3y=5 is a linear equation in standard form. When an equation is given in this form, it's pretty easy to find both intercepts (x and y). This form is also very useful when solving systems of two linear equations.