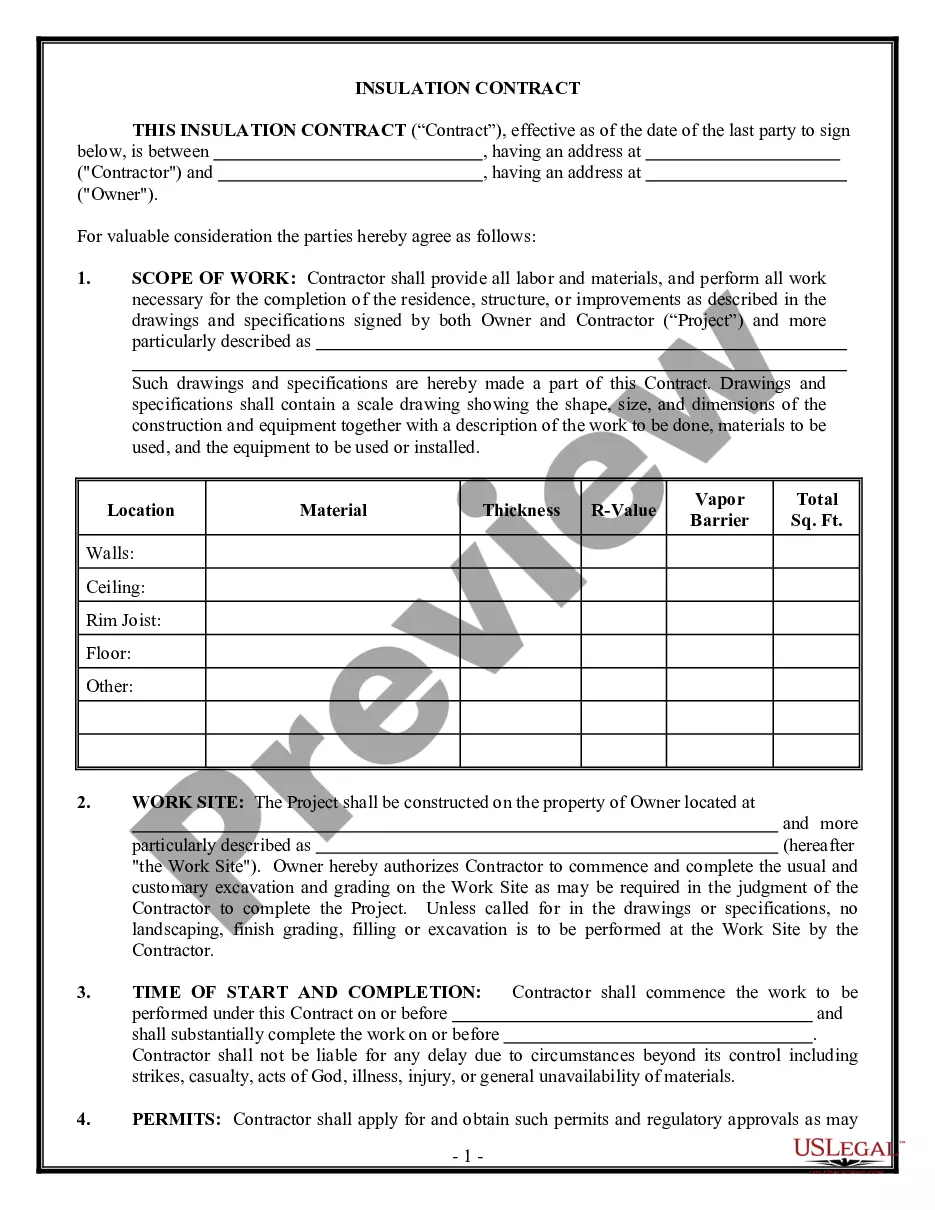
Closure Any Property For Addition In Orange
Description
Form popularity
FAQ
Closure property of addition states that in a defined set, for example, the set of all positive numbers is closed with respect to addition since the sum obtained adding any 2 positive numbers is also a positive number which is a part of the same set.
Closure Property: When something is closed, the output will be the same type of object as the inputs. For instance, adding two integers will output an integer. Adding two polynomials will output a polynomial. Addition, subtraction, and multiplication of integers and polynomials are closed operations.
Closure Property for Integers The set of integers is given by Z = { … , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , … } . The closure property holds true for addition, subtraction, and multiplication of integers. It does not apply for the division of two integers.
Closure Property of Addition for Whole Numbers Addition of any two whole numbers results in a whole number only. We can represent it as a + b = W, where a and b are any two whole numbers, and W is the whole number set. For example, 0+21=21, here all numbers fall under the whole number set.
The closure property of addition states that when any two elements of a set are added, their sum will also be present in that set. The closure property formula for addition for a given set S is: ∀ a, b ∈ S ⇒ a + b ∈ S.
The closure property is applicable for addition and multiplication for most of the number systems. In spite of that, for subtraction and division, some sets are not closed.
The addition is the process of adding 2 or more numbers to get a final result. The 4 main properties of addition are commutative, associative, distributive, and additive identity.
Closure property holds for addition, subtraction and multiplication of integers. Closure property of integers under addition: The sum of any two integers will always be an integer, i.e. if a and b are any two integers, a + b will be an integer.
The sum of any two real numbers will result in a real number. This is known as the closure property of addition. The result will always be a real number. In general, the closure property states that the sum of any two real numbers is a unique real number.
When adding three numbers, changing the grouping of the numbers does not change the result. This is known as the Associative Property of Addition.