Closure Any Property With Polynomials In Queens
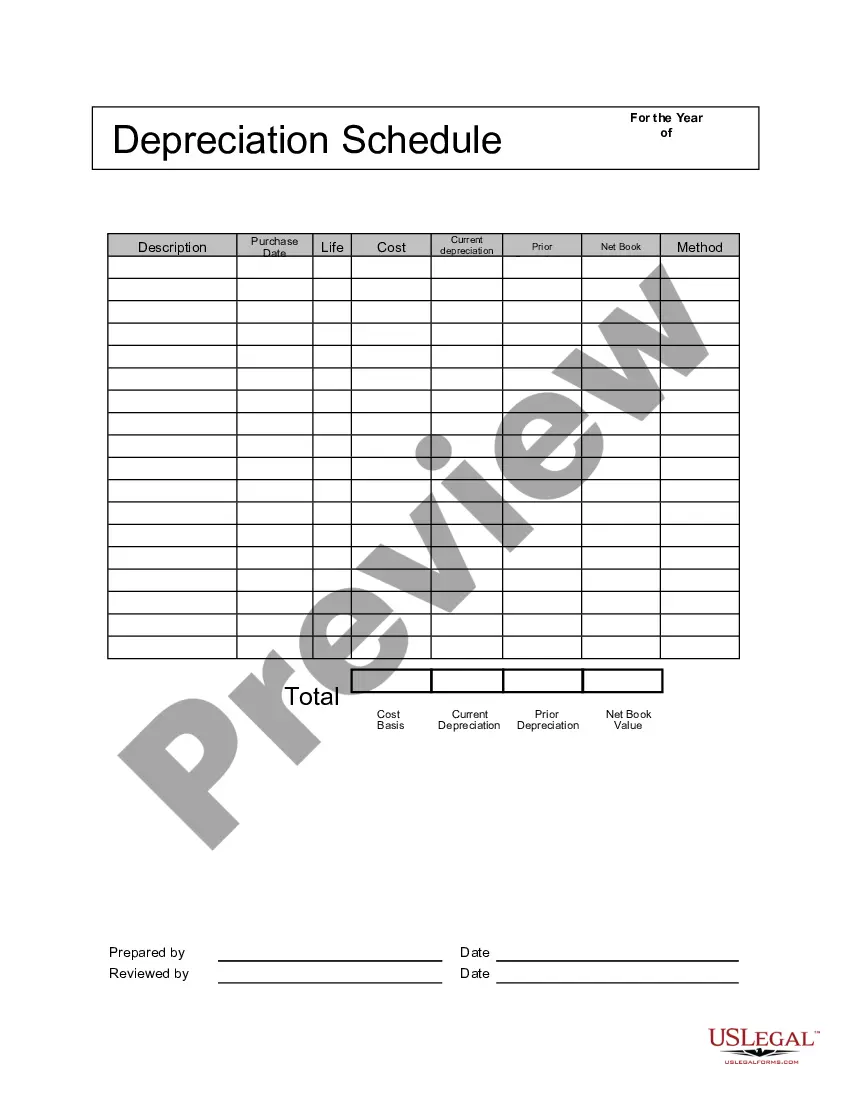
Description
Form popularity
FAQ
When a integer is divided by another integer, the result is not necessarily a integer. Thus, integers are not closed under division.
Closure Property: When something is closed, the output will be the same type of object as the inputs. For instance, adding two integers will output an integer. Adding two polynomials will output a polynomial. Addition, subtraction, and multiplication of integers and polynomials are closed operations.
CLOSURE: Polynomials will be closed under an operation if the operation produces another polynomial. Adding polynomials creates another polynomial. Subtracting polynomials creates another polynomail. Multiplying polynomials creates another polynomial.
The closure property of integers does not hold true for the division of integers as the division of two integers may not always result in an integer. For example, we know that 3 and 4 are integers but 3 ÷ 4 = 0.75 which is not an integer. Therefore, the closure property is not applicable to the division of integers.
The closure property for polynomials states that the sum, difference, and product of two polynomials is also a polynomial. However, the closure property does not hold for division, as dividing two polynomials does not always result in a polynomial. Consider the following example: Let P(x)=x2+1 and Q(x)=x.
Polynomials are NOT closed under division (as you may get a variable in the denominator).
4) Division of Rational Numbers The closure property states that for any two rational numbers a and b, a ÷ b is also a rational number. The result is a rational number. But we know that any rational number a, a ÷ 0 is not defined. So rational numbers are not closed under division.
If we add two integers, subtract one from the other, or multiply them, the result is another integer. The same thing is true for polynomials: combining polynomials by adding, subtracting, or multiplying will always give us another polynomial.
Ing to the Associative property, when 3 or more numbers are added or multiplied, the result (sum or the product) remains the same even if the numbers are grouped in a different way. Here, grouping is done with the help of brackets. This can be expressed as, a × (b × c) = (a × b) × c and a + (b + c) = (a + b) + c.
CLOSURE: Polynomials will be closed under an operation if the operation produces another polynomial. Adding polynomials creates another polynomial. Subtracting polynomials creates another polynomail. Multiplying polynomials creates another polynomial.