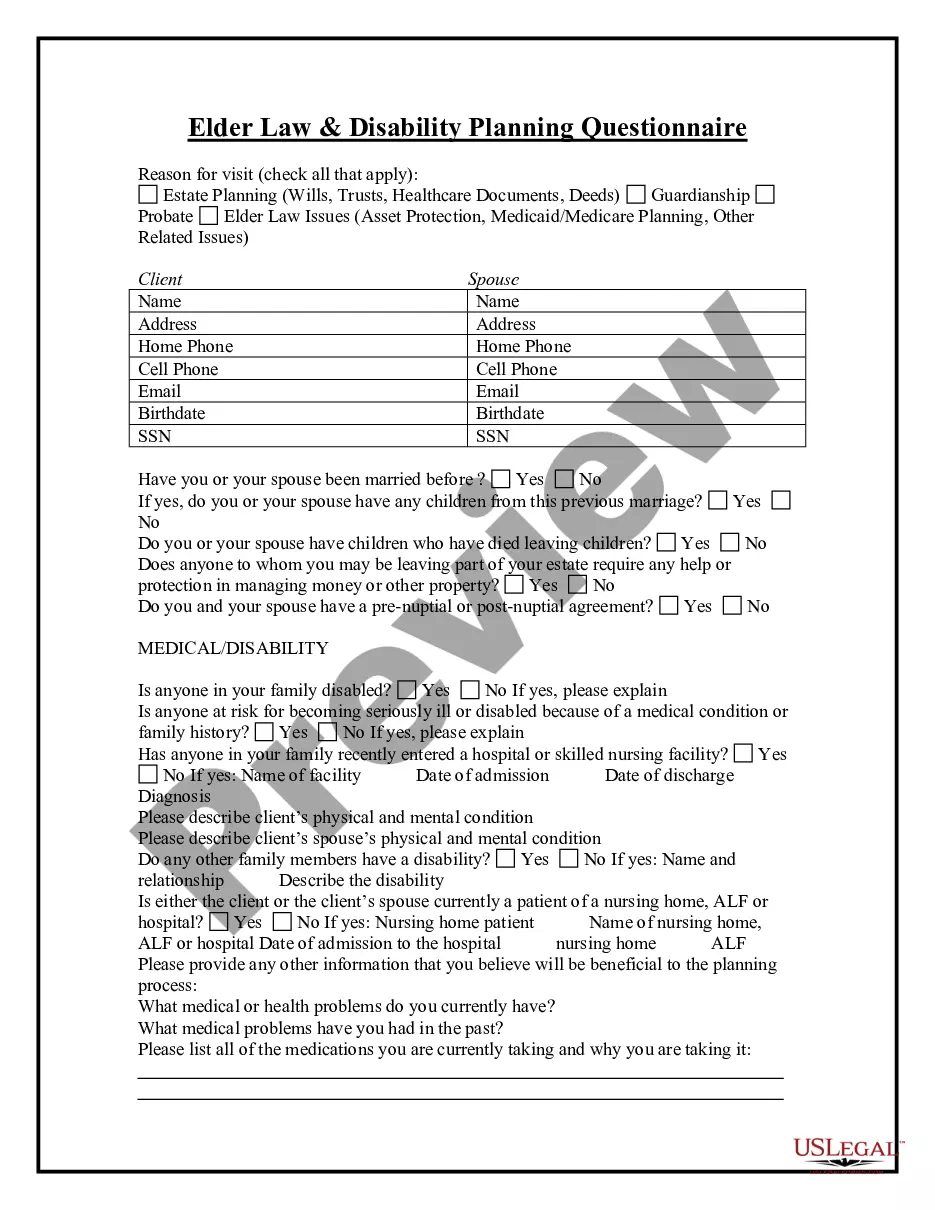
Closure Any Property With Polynomials In Phoenix
Description
Form popularity
FAQ
The closure property of addition states that when any two elements of a set are added, their sum will also be present in that set. The closure property formula for addition for a given set S is: ∀ a, b ∈ S ⇒ a + b ∈ S.
Polynomial Vector Space The concept of a vector space is foundational in linear algebra and is characterized by a set of axioms that polynomials satisfy, such as closure under addition and scalar multiplication—a vector space is essentially a playground where polynomials can interact seamlessly under these operations.
The closure property for polynomials states that the sum, difference, and product of two polynomials is also a polynomial. However, the closure property does not hold for division, as dividing two polynomials does not always result in a polynomial. Consider the following example: Let P(x)=x2+1 and Q(x)=x.
Closure Property: When something is closed, the output will be the same type of object as the inputs. For instance, adding two integers will output an integer. Adding two polynomials will output a polynomial.
Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication, and also positive integer exponents for polynomial expressions but not division by variable.
Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials.
In mathematics, the set of polynomials is not closed under division. This is because when you divide one polynomial by another, the result may not always be a polynomial. For instance, if we consider the polynomials P(x) = x2 and Q(x) = x.
Polynomials are closed under addition, subtraction, and multiplication. Polynomials are not closed under division.
Closure Property: When something is closed, the output will be the same type of object as the inputs. For instance, adding two integers will output an integer. Adding two polynomials will output a polynomial. Addition, subtraction, and multiplication of integers and polynomials are closed operations.