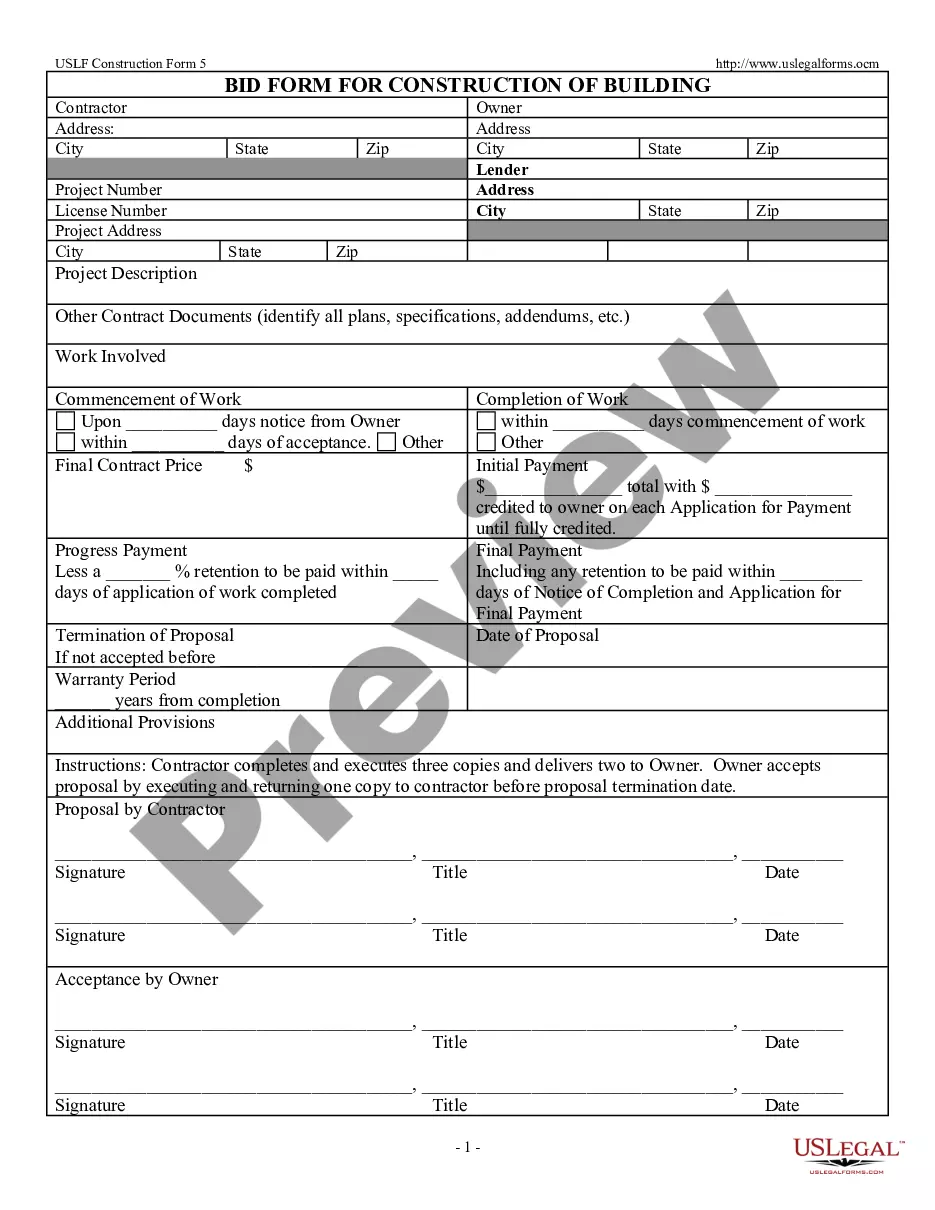
This is a generic form for the sale of residential real estate. Please check your state=s law regarding the sale of residential real estate to insure that no deletions or additions need to be made to the form. This form has a contingency that the Buyers= mortgage loan be approved. A possible cap is placed on the amount of closing costs that the Sellers will have to pay. Buyers represent that they have inspected and examined the property and all improvements and accept the property in its "as is" and present condition.
Sell Closure Property For Integers In Kings
Category:
State:
Multi-State
County:
Kings
Control #:
US-00447BG
Format:
Word
Instant download
Description
Free preview
Form popularity
FAQ
The set of integers is not closed under the operation of division. because when one intger is divided by another integer,the result is not always an integer. For example, 4 and 9 both are integers, but 4 ÷ 9 = 4/9 is not an integer. Q.
Among the various properties of integers, closure property under addition and subtraction states that the sum or difference of any two integers will always be an integer i.e. if x and y are any two integers, x + y and x − y will also be an integer.
Lesson Summary If the division of two numbers from a set always produces a number in the set, we have closure under division. The set of whole numbers are not closed under division, and the set of integers are not closed under division because they both produce fractions.
Do you know why division is not under closure property? The division is not under closure property because division by zero is not defined. We can also say that except '0' all numbers are closed under division.
RULE 1: The quotient of a positive integer and a negative integer is negative. RULE 2: The quotient of two positive integers is positive. RULE 3: The quotient of two negative integers is positive.
The closure property of addition states that when any two elements of a set are added, their sum will also be present in that set. The closure property formula for addition for a given set S is: ∀ a, b ∈ S ⇒ a + b ∈ S.
Among the various properties of integers, closure property under addition and subtraction states that the sum or difference of any two integers will always be an integer i.e. if x and y are any two integers, x + y and x − y will also be an integer.
Properties of Subtraction Closure Property: The closure property of subtraction tells us that when we subtract two Whole Numbers, the result may not always be a whole number. For example, 5 - 9 = -4, the result is not a whole number.
The closure property of addition states that when any two elements of a set are added, their sum will also be present in that set. The closure property formula for addition for a given set S is: ∀ a, b ∈ S ⇒ a + b ∈ S.
More info
Closure property under multiplication states that the product of any two integers will be an integer i.e. The document discusses the properties of integers.Integers include positive and negative whole numbers along with zero. These questions will help students practise and master the basics of integers. This activity is a great way for students to analyze the relationship between sets of numbers and the closure property. The sum of any two integers will always be an integer, i.e. Help you fill out your documents; Determine the legal correctness of your document; Accept illegible documents. Are you in the right place? For assistance speak to any member of station staff or contact the British Transport Police on 0800 40 50 40 (24 hours) or text 61016. In an emergency call 999.