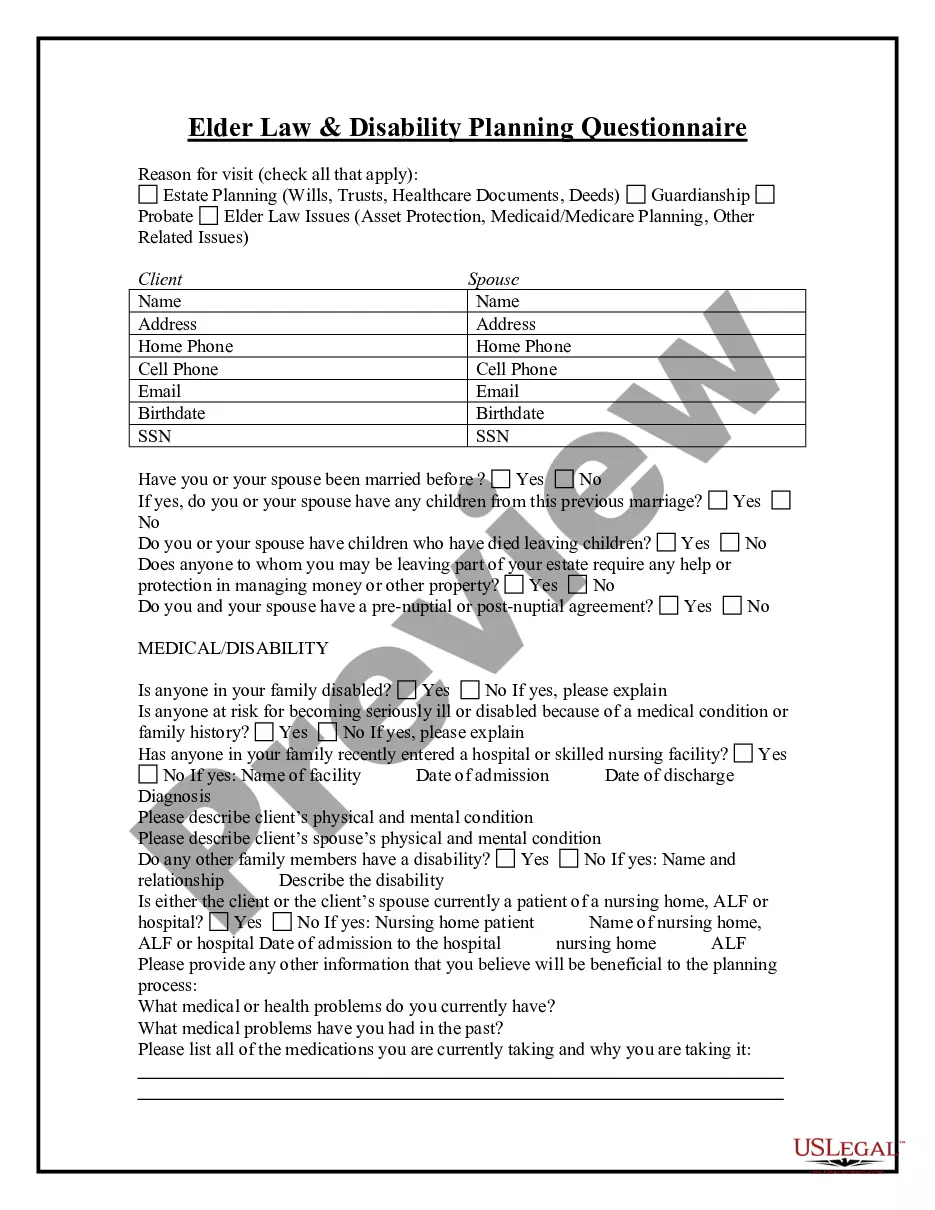
Elder Form With 2 Points In Collin
Description
Form popularity
FAQ
It. Positive over 6 which equals uh divide you'll have a -4/3. So now we know m. Equal a -4/3. SoMoreIt. Positive over 6 which equals uh divide you'll have a -4/3. So now we know m. Equal a -4/3. So when writing my equation using my point slope form I'm going to now put -4/3 in for M.
Answer so this is the equation. In point slope. Form. But now let's get the answer in slopeMoreAnswer so this is the equation. In point slope. Form. But now let's get the answer in slope intercept. Form. So let's distribute the two. It's going to be 2X. And then 2 -5 that's -10.
The application of the 2-point method to predict the 1RM requires 3 simple steps: (a) to set the task specific velocity of the 1RM preferably recorded in previous studies, (b) record the mean velocity against 2 different external loads representing approximately 50 and 80% of self-reported 1RM, and (c) model the ...
To write equation of a line in two-point form, simply substitute the coordinates of the given two points in the equation ( y − y 2 ) = y 2 − y 1 x 2 − x 1 ( x − x 2 ) . Example: Find the equation of a line passing through the points and . Substitute the values in ( y − y 2 ) = y 2 − y 1 x 2 − x 1 ( x − x 2 ) .
To write equation of a line in two-point form, simply substitute the coordinates of the given two points in the equation ( y − y 2 ) = y 2 − y 1 x 2 − x 1 ( x − x 2 ) . Example: Find the equation of a line passing through the points and . Substitute the values in ( y − y 2 ) = y 2 − y 1 x 2 − x 1 ( x − x 2 ) .
In general form they would be the same. So you can use whichever you prefer. So I'm going to say yMoreIn general form they would be the same. So you can use whichever you prefer. So I'm going to say y minus 6. Equals now my slope is up here negative eight over three times x minus X1 was 1..
Given two points on a line, we can write an equation for that line by finding the slope between those points, then solving for the y-intercept in the slope-intercept equation y=mx+b.
Point-slope form: y-a = m(x-b). For example, your slope (m) is 3 and your point (a,b) is 9,10. You would substitute your y-coordinate for a, and your x- coordinate for b. Your new equation would look like this: y-10 = 3(x-9).