Get Alg 1 A.7 Graphing Quadratics Notes - Lcps.org

The Alg 1 A.7 Graphing Quadratics Notes document provides essential information for understanding quadratic functions and their graphs. This guide will walk you through the process of filling out the document online, ensuring you have all the necessary components for a complete understanding of the material.

Follow the steps to accurately complete the form.

1. Press the ‘Get Form’ button to access the form and open it in the online editor.
2. Begin by entering your name in the designated field, ensuring you provide your full name for proper identification.
3. Next, fill in the date on which you are completing the document. This is typically placed next to your name.
4. In the block section, indicate the class block you are associated with.
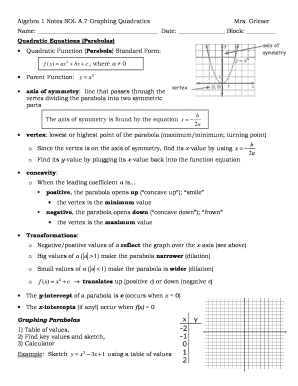
5. Review the section on quadratic equations, taking note of the standard form of a quadratic function, the parent function, and definitions provided for terms such as axis of symmetry, vertex, and concavity.
6. For graphing, follow the instructions to sketch graphs based on example functions. Populate the relevant fields with concavity, y-intercept, axis of symmetry, vertex, and zeros as you go.
7. Utilize the examples provided to guide your sketches, ensuring to find key values where necessary.
8. Complete the ‘You Try’ section by sketching the graphs of the provided functions and finding the requested information, filling in concavity, y-intercepts, axis of symmetry, vertices, and zeros.
9. Once you have filled in all necessary fields, review the document for completeness and accuracy.
10. Finally, you can save your changes, download the document, print it, or share it as required.

Start filling out your Alg 1 A.7 Graphing Quadratics Notes document online today!