Get Postulates
How it works
-
Open form follow the instructions
-
Easily sign the form with your finger
-
Send filled & signed form or save
How to fill out the Postulates online
This guide provides step-by-step instructions on how to fill out the Postulates online effectively. Whether you're familiar with such documents or new to them, this guide will equip you with the necessary skills to complete the form accurately.
Follow the steps to complete the Postulates form online
- Click ‘Get Form’ button to obtain the form and open it for editing.
- Begin filling out your name, the date, and section labeled 'Pd'. These fields are usually located at the top of the document and require your personal identification and the current date for record-keeping.
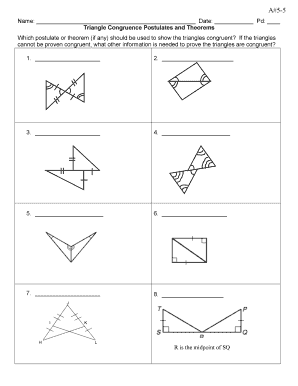
- Proceed to the section for Triangle Congruence Postulates and Theorems. You will need to analyze the triangles presented and note which postulate or theorem can demonstrate their congruence. Fill each blank with the appropriate postulates as you assess the information provided.
- Mark the drawing to reflect the given information. This step is crucial for visual representation; ensure you accurately depict all relevant angles and sides.
- For questions requiring proof of triangle congruence, move on to complete those sections. Fill in the blanks logically based on your previous marks. This may involve writing the congruence statement for each set of triangles denoted.
- Continue filling out the proof sections methodically. For each proof, detail your statement and reason clearly. This documentation is essential to validate the logical steps leading to your conclusion.
- Once you have completed all sections of the form, review it for accuracy. Ensure all statements and justifications are complete and well-supported.
- Finally, you can save the document, download it for your records, print it out, or share it as needed.
Complete the Postulates online today to ensure your triangles are analyzed accurately.
In science, a postulate is a basic assumption that serves as a foundation for scientific theories and experiments. It provides a starting point for hypotheses and further inquiry. For example, many scientific postulates relate to the laws of nature, forming the basis for how we understand the universe. By grounding our scientific inquiries in verified postulates, we can build a more accurate and reliable framework for testing and discovering new information.
Industry-leading security and compliance
-
In businnes since 199725+ years providing professional legal documents.
-
Accredited businessGuarantees that a business meets BBB accreditation standards in the US and Canada.
-
Secured by BraintreeValidated Level 1 PCI DSS compliant payment gateway that accepts most major credit and debit card brands from across the globe.


